| Název | Minimalizace |
|---|---|
| Autor | Neznámý |
| Naposledy upravil | Lukáš Hozda |
| Poslední změna | 2021-01-24 22:53:14 +0100 |
| Předmět | Unixové operační systémy |
Minimalizace
V tomto příkladu si vytvoříme driver jednoho segmentu sedmi-segmentového displeje a provedeme jeho minimalizaci.
Vytvoření driveru
Vybereme se jeden segment z displeje, pro který navrhneme driver.
 {height=100px}
{height=100px}
Pro popis hodnot od 0 do 9 potřebujeme 4 bity - potřebujeme tedy 4 vstupy. Jako první je třeba vypsat stavy, při kterých bude segment svítit. Vypíšeme si tedy 4-bitová binární čísla s hodnotami 0 až 9.
x A B C D
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
A, B, C a D jsou naše 4 vstupy a x je pouze hodnota v desítkové soustavě. Nyní musíme přidat výstupní bit Q, který nám definuje, při jaké hodnotě bude segment rozsvícen. U čísla 0 svítit bude, ale například u čísla 5 ne.
x A B C D Q
0 0 0 0 0 1
1 0 0 0 1 1
2 0 0 1 0 1
3 0 0 1 1 1
4 0 1 0 0 1
5 0 1 0 1 0
6 0 1 1 0 0
7 0 1 1 1 1
8 1 0 0 0 1
9 1 0 0 1 1
Sice nám zbývají další nevyužité hodnoty (10, 11, 12 atd.), ale u těch je nám nezáleží na jejich stavu. To se nám hodí později při minimalizaci.
Nyní si vypíšeme funkci, která popisuje všechny stavy, při kterých bude segment svítit. Například hned u stavu s hodnotou 1 svítit bude, proto popíšeme stavy vstupů jako $\bar{A}\bar{B}\bar{C}D$. Vstupy s hodnotou 0 označíme čarou nad písmenem, což je NOT. Znaménko $$ samozřejmě označuje AND a znaménko $+$ značí OR.
$$ f(x) = \ \bar{A}\bar{B}\bar{C}\bar{D} + \ \bar{A}\bar{B}\bar{C}D + \ \bar{A}\bar{B}C\bar{D} + \ \bar{A}\bar{B}CD + \ \bar{A}B\bar{C}\bar{D} + \ \bar{A}B\bar{C}D + \ \bar{A}BC\bar{D} + \\bar{A}BCD + \ A*\bar{B}\bar{C}\bar{D} + \ A*\bar{B}*\bar{C}*D $$
A máme hotový vzorec pro implementaci jednoho segmentu. Pokud bychom ale chtěli tuto věc implementovat, potřebovali bychom 25 NOTů, 30 ANDů a 9 ORů, to je celých 64 součástek!!!? Proto je dobré provést minimalizaci.
Minimalizace
Minimalizace nám pomůže zjednodušit náš vzorec pro implementaci a v reálném světě nám ušetří spousty peněz za součástky.
V našem případě využijeme Karnaughovu mapu o velikosti $4*4$.
 {width=300px}
{width=300px}
Do mapy doplníme všechny stavy při hodnotách 0 až 9 z naší první tabulky z výstupy Q. Mapa se vyplňuje tak, že musíme najít jeden společný průnik všech vstupů. Začneme vstupem A. Ten má na hodnotu 0, vybereme tedy bloky v mapě, pro které platí, že A je 0.
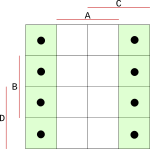 {width=150px}
{width=150px}
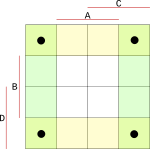 {width=150px}
{width=150px}
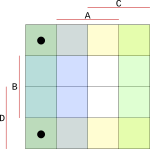 {width=150px}
{width=150px}
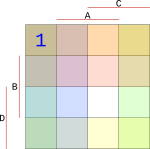 {width=150px}
{width=150px}
\newpage
Do bloku, na který jsme narazili sečtením všech průniků, zapíšeme hodnotu zda segment svítí nebo nesvítí. Protože jsme hledali blok pro desítkovou hodnotu 0, při které bude segment svítit, dáme do mapy hodnotu 1 (bude svítit). Stejným postupem vyplníme celou tabulku pro zbylé hodnoty 1 až 9.
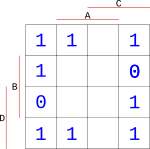 {width=150px}
{width=150px}
Pro minimalizaci musíme seskupit všechny hodnoty 1 do skupin nejlépe po čtyřech. Čím větší bloky, tím větší zjednodušení výsledku.
Pro Karnaughovu mapu platí, že hodnoty lze seskupovat i přes hrany, či přes rohy. Detaily o tom proč a jak toto funguje jsou popsány například na wikipedii.
Další specialita mapy je ta, že nevyplněné bloky si můžeme doplnit podle potřeby. Vzpomeňte si na začátek dokumentu, kde nám zbylo několik nevyužitých hodnot pro čísla 11, 12 atd. U těch je nám jedno, v jakém stavu budou, a proto si je do mapy můžeme doplnit podle sebe a tím si uměle vytvořit lepší bloky pro minimalizaci.
První blok se nám nabízí například vlevo nahoře, kde si můžeme doplnit jedničku a vytvořit blok $2*2$.
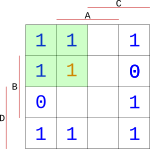 {width=150px}
{width=150px}
Dále můžeme využít to, že bloky lze vytvářet i přes rohy. V každém rohu se nachází 1, tak je dáme do dalšího bloku.
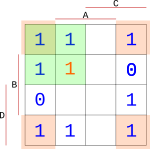 {width=150px}
{width=150px}
\newpage
Tímto způsobem dotvoříme zbytek bloků, dokud nebudou v blocích všechny námi vypsané (modré) jedničky.
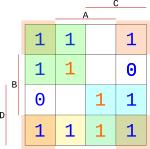 {width=150px}
{width=150px}
Všechny bloky teď popíšeme do vzorce. Protože bloky jsou o velikosti $2*2$, stačí nám na popis každého bloku pouze dva vstupy.
$$ f(x) = \bar{C}\bar{D} + \bar{A}\bar{B} + DC + D\bar{B} $$
To dám dohromady dává pouze 12 součástek. Základní minimalizace je kompletní.